- Most limnological phenomena, distribution of biota, and productivity are directly related to the morphological features of the water basin. While many aspects of a lakes fauna and flora can be studied without this knowledge, to venture into theoretical limnology and to determine some indices of productivity, morphometric data must be known.
- Mapping of the water basin should be the centerpiece of any comprehensive study of a pond. Calculations made from the map will allow the investigator to accumulate and relate a lot of data concerning the pond system.
- The purpose of this project information is to help the environmental science student organize an extended project. This is a direct measurement method, intended for a smaller body of water.
MATERIALS:
Survey transit, tripod, outfit
Nails, plastic survey ribbon, survey flags, 2 iron rods
Plastic (floating) rope
Yarn
Measuring tape (metric)
3 meter sticks
1 x 2 inch strip of lumber the length of the 3 meter sticks
Small metal plate
Sounding line marked in meters
Small boat or inflatable raft
Safety equipment (Life vest)
Graph paper (in an appropriate grid size to construct a scale drawing)
Large clipboard to use in the field
Drafting equipment as neededREFERENCE:
- Any study is only as good as the preparation you do for it. Good reference material is critical to this project. I highly recommend the following college Limnology text book:
-
Cole, Gerald A.. 1983. Textbook of Limnology. Third edition. The C. V. Mosby Company. St. Louis, Missouri: 401 pp.
PROCEDURE:
Preparation
- Prepare the floating plastic rope for the study. This needs to be long enough to cross the pond and attach to the two rods. It becomes lines of your grid, which are marked for the other grid direction and soundings.
- Make a loop in one end, to be slid over the iron rod on the base line. Stretch it out between the two rods at the same tension you plan to use in the study. Now measure off lengths along the rope at the appropriate grid size you intend to use. Every 3 meters is a good suggested size. The yarn is used to mark the rope at the measured distances. Slide the yarn through the weave of the rope and then tie it securely around the measured point. Leave a little amount on the ends for visibility.
- Put graph paper together that will be larger than the pond drawing. You will mark shore line and depth soundings directly on this graph. Record the scale you are using directly on this graph paper (ie. 1 centimeter = 1 meter).
- Make a sounding rod by attaching the three meter sticks to the 1 x 2 inch lumber, and attaching the small metal plate on the bottom. This is a faster and easier way of taking depth soundings in shallower water than with a sounding line.
Study site
- When using a transit, always level the transit for each use. Otherwise, distances and angles will be incorrect.
- A base line is shot with the transit and marked every 3 meters (or the distance you have chosen). Use nails with a small piece of bright colored plastic survey ribbon to mark these points. Be sure to protect your first mark (bench mark), it is the point that all other measurements are related to.
- Write down the angle the baseline makes with respect to the compass points, so you will be able to indicate compass points on your map.
- Placing the transit, in turn, over each mark on the baseline, shoot parallel lines across the pond at right angles to the base line. Use survey flags to mark the lines on the opposite side of the pond from the baseline.
- Stretch the cord, marked in 3 meter intervals, across the pond between corresponding points on the parallel lines. This rope is used to place the soundings at the three meter square intervals on the grid. Do this directly with the sounding rod or line, from the boat. Remember to wear a life jacket. Record depth to the nearest 0.1 Meter. Mark the shore line and the depth soundings directly on the graph paper. Be sure you mark them on the correct corresponding grid point of the paper.
Classroom
- Smoothly connect the measured marks for the shore line on the graph paper to establish the outline of the pond. You have to decide how often you will draw an isobath line (line of equal depth). On a small pond, isobaths every 0.5 meters is usually a good choice. If the pond is deep and falls off quickly, you may want isobaths every 1 meter.
- To find the location of the isobath line on your graph, you just have to use a formula derived from cross multiplication.
For example: If 3 grid lines go from a depth of 0.8 meters to a depth of 1.7 meters.
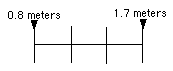
To mark where the 1.5 meter isobath goes, first find the differences between 0.8 meters and the other two depths.
1.7 - 0.8 = 0.9 meters
1.5 - 0.8 = 0.7 meters
The cross multiplication equality is then:
3 grid lines
0.9 meters= X
0.7 metersRearranging to solve for X, you get:
(3 grid lines )(0.7 meters )
0.9 meters= X This gives you a distance of 2.3 graph lines from the shallower depth for the location of the 1.5 meter isobath line.
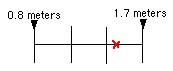
Smoothly connect all the marks for each isobath on the working graph as you did for the shore line. Mark the maximum depth point also.
- Using good drafting paper, with pre-printed border and information block if possible, trace the final map directly off the working graph grid. Draw a north arrow on the drawing, using the degree information you made from the base line. Put the scale on the map. A bar scale is a good way to represent this.
- A number of morphometric data can be calculated from your map. Cole, in his text book, explains how to calculate the following: Maximum length, Maximum breadth, Mean width, Surface area, Length of shoreline, Shoreline development index, Maximum depth, Mean depth, Relative depth, Volume, and Volume development index. Also Basin slope between isobaths can be calculated.
- The following are the formulas and instructions for calculating the morphometric data listed above. Refer to Cole, or another source for further information and explanation of these measurements.
Maximum length (l)
- The distance across the water between the two most separated points on the shore line is the maximum length. You simply measure this from your map, convert the measurement with your scale, and record it.
Maximum breadth or width (b)
- This is the distance between the most separated points on the shore line, measured at 90 degrees to the line of maximum length.
Mean width (
 )
)
- This is the quotient of area divided by maximum length.

- Using fine drafting paper (that has very uniform density), like that used to make your map, trace off the pond outline very lightly. Cut out the pond image you traced. Now cut a square from the same piece of drafting paper that represents a known area according to your scale. A square representing 100 m2 is a good size. Using an accurate balance, find the mass of the known area square. Divide this mass by the number of square meters it represents. This gives you the mass of 1 square meter. Now find the mass of the pond image. Dividing the mass of the pond image by the mass representing 1m2, will give you the area of your pond in square meters.
Length of shoreline (L)
- The length of the shoreline can be determined by using a string and laying it on the map, along the shoreline of the map. Then measure the length of the string and adjust to meters from your scale.
Shoreline development index (DL)
- The development of the shoreline is a comparative figure relating the shoreline length to the circumference of a circle that has the same area as the pond. The smallest possible index would be 1.0. For the following formula, both L and A must be in consistent units for this comparison---meters and square meters.

- This is simply taken from your raw data on measuring the depth of the pond. It is the maximum depth you measured.
relative depth (zr)
- This is the ratio of the maximum depth in meters to the average diameter of the pond surface. The following equation has the computation for percentage built into it, for the ratio is expressed in that manner.

- The volume of a pond can be calculated when the area circumscribed by each isobath is known. The formula for the first volume calculation, the volume of water between the shoreline contour (z0) and the first subsurface contour (z1), is as follows:

- Trace the pond again lightly on fine drafting paper, as before, but this time lightly trace all the contour lines, and mark the maximum depth point. Calculate each area as you did before. To calculate Az1, cut off the portion of the pond image outside the first subsurface contour line. Plug in the appropriate data to the formula, and calculate each volume section. The last area is that inside the last subsurface contour line, and the last depth used is the maximum depth zm. Add all the calculated volumes together to arrive at the volume of the pond.
Mean depth (
 )
)
- The pond volume divided by its surface area will yield the mean depth. Remember to keep units the same. If volume is in cubic meters, then area must be in square meters. The equation would be:

- This compares the shape of the basin to an inverted cone with a height equal to zm and a base equal to the ponds surface area. If the pond had a volume equal to this hypothetical cone, DV would equal 1.0. If the pond volume was greater, the index would be greater than 1.0, and if the pond volume was less than the cone, the index would be below 1.0. Since the actual volume of the lake is A(
 ), the ratio of actual volume to the volume of the theoretical cone is expressed as:
), the ratio of actual volume to the volume of the theoretical cone is expressed as:


- If the pond has a spring or other source, and discharges water regularly, you can calculate the flow rate by whatever means is appropriate to your situation, and add this data to your paper.
GOOD LUCK and enjoy this study!!
Back to Environmental Science Table of Contents
Back to Lab Dad's Laboratory
- Mapping of the water basin should be the centerpiece of any comprehensive study of a pond. Calculations made from the map will allow the investigator to accumulate and relate a lot of data concerning the pond system.
CONSTRUCTING A
BATHYMETRIC MAP
OF A POND OR SMALL LAKE
INTRODUCTION: