Esta é uma pequena descrição para ilustrar as ondas e sua velocidade de propagação.

O conceito de onda em física, pode ser dito como a ''perturbação oscilante de alguma grandeza física no espaço e periódica no tempo''. Assim temos uma oscilação espacial caracterizada por um ''comprimento de onda'' e uma ''periodicidade no tempo, ''que é medida pela freqüência, que é definida como o inverso do seu período”. Uma onda é um pulso energético que se propaga através do espaço ou através de um meio (líquido, sólido, gasoso, vácuo). Ondas eletromagnéticas, neutrinos, etc, se propagam através da matéria onde as partículas do meio oscilam à volta de um ponto médio, mas não se deslocam.

A radiação eletromagnética, e provavelmente as ondas gravitacionais, podem se propagar através do vácuo, contudo as ondas existem inclusive num meio cuja deformação é capaz de produzir forças de restauração através das quais elas viajam e podem transferir energia de um lugar para outro sem que qualquer das particulas do meio seja deslocada permanentemente como acontece num imã; isto é, nenhuma massa transportada associada pode anular o efeito magnético. Em lugar disso, qualquer ponto particular oscila em volta de um ponto fixo.

Características:

Uma onda pode voltar para a direção de onde veio, devida batida num anteparo ou material reflexivo, a este fenômeno chamamos ''reflexão''. Também pode ocorrer a sua mudança de direção, devida sua propagação em meios de diferentes densidades, chamado de ''refração''. Quando há o espalhamento das ondas, por exemplo quando atravessam uma fenda de tamanho equivalente a seu comprimento, ocorre o fenômeno da ''difração''. Ao ocorredr a adição das amplitudes de duas ondas que se superpõe, ocorre a interferência. Se acontece a separação de uma onda em outras de diferentes freqüências, temos a ''dispersão''.

Ondas transversais e longitudinais e polarização.

As transversais são aquelas em que a vibração é perpendicular à direção de sua propagação, nunca podem ser polarizadas e podem oscilar em qualquer direção no plano perpendicular à direção de propagação. As ondas longitudinais são aquelas em que a vibração ocorre na mesma direção do movimento. As ondas polarizadas no entanto, oscilam em apenas uma direção perpendicular à linha de propagação.

Onda, Freqüência e Comprimento de onda

Freqüência (F) é período dividido por uma unidade de tempo (exemplo: um segundo), e é expressa em hertz.

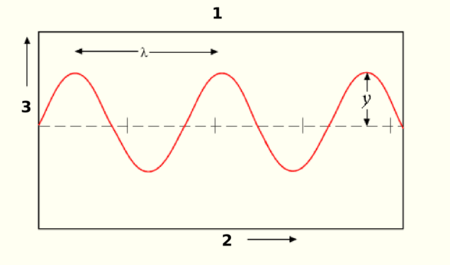
1 = Elementos de uma onda

2 = Distância

3 = Deslocamento

= Comprimento de onda

Y = Amplitude

Quando ondas são expressas matematicamente, a freqüência angular (ômega; radianos por segundo) é constantemente usada, relacionada com freqüência f em:

Quando temos ondas não estacionárias que se movem num meio, estas têm uma perturbação que varia tanto com o tempo ''t'' quanto com a distância ''z'' e pode ser expressa:

onde A(z,t) é o envelope de amplitude da onda, k é o número de onda e f é a fase. A velocidade v desta onda é dada por:

onde é o comprimento de onda (Embaixo).

Comprimento de onda:

Observe que no gráfico, o eixo x representa a distância

( ) e o eixo y é chamado de amplitude da onda.

O

Assim, tem uma relação inversa com a frequência f, que é a quantidade de repetição de qualquer fenômeno em determinado tempo.

O comprimento de onda é igual à velocidade da onda dividida pela frequência. No caso da radiação eletromagnética no vácuo, esta é igual à velocidade da luz ''c'', para sinais propagados pela atmosfera, esta relação é dada por:

= c / f

onde:

= comprimento de onda de uma onda eletromagnética;

c = velocidade da luz no váculo = 299.792,458 km/s ~ 300.000 km/s = 300.000.000 m/s ou

[ ** Para o caso do som c = velocidade do som no ar = 343 m/s a 20 °C (68 °F)];

f = frequência da onda 1/s = Hz.

A velocidade de uma onda pode ser calculada com a seguinte fórmula:

v = / T

onde:

v = velocidade da onda.

= comprimento de onda;

T = período da onda.

O inverso do período, 1/T, é chamado de freqüência:

f = 1 / T

e mede o número de ''ciclos'' (''repetições'') por segundo executados pela onda, dada em Hertz (ciclos/segundo). Para caracterizar uma onda, portanto, é necessário conhecer apenas duas quantidades, a velocidade e o comprimento de onda ou a frequência e a velocidade, já que a terceira quantidade pode ser determinada da equação acima, que podemos reescrever como:

f = v /

Quando ondas de luz (e outras ondas eletromagnéticas) entram num dado meio, o seu comprimento de onda é reduzido por um fator igual ao índice de refração ''n'' do meio, mas a frequência permanece inalterada. O comprimento de onda no meio, é dado por:

' = o / n

Amplitude

A amplitude de uma onda é a medida da magnitude de um distúrbio num meio durante um ciclo. Por exemplo, ondas em uma corda a tem expressa como uma distância (metros), ondas de som como pressão (pascals) e ondas eletromagnéticas como a amplitude de um campo elétrico (volts por metro).

Pode ser constante (neste caso a onda é uma onda contínua), ou pode variar com tempo e/ou posição. A forma desta variação é o envelope da onda.

A distância Y, é a amplitude da onda, também conhecida como "pico de amplitude" para distingüi-la de outro conceito usado em engenharia elétrica: root mean square amplitude (ou amplitude rms), definida como a raiz quadrada da média temporal da distância vertical entre o gráfico e o eixo horiontal.

O uso de "pico de amplitude" não é ambíguo para ondas simétricas e periódicas como senóides, onda quadrada e onda triangular. Para ondas sem simetria, por exemplo pulsos periódicos em uma direção, o termo "pico de amplitude" torna-se ambíguo pois o valor obtido é diferente dependendo se o máximo valor positivo é medido em relação à média, se o máximo valor negativo é medido em relação à média ou se o máximo sinal positivo é medido em relação ao máximo sinal negativo e dividido por dois. Para ondas complexas, especialmente sinais sem repetição tais como ruído, a amplitude rms é usada frequentemente porque não tem essa ambiguidade e também porque tem um sentido físico. Por exemplo, a potência transmitida por uma onda acústica ou eletromagnética ou por um sinal elétrico é proporcional à raiz quadrada da amplitude rms (e em geral, não tem essa relação com a raiz do pico de amplitude)

Período

O Período é definido como ''o tempo necessário para que um movimento realizado por um corpo volte a se repetir''. Num relógio de pêndulo, por exemplo, o período é determinado pelo ''tempo'' que a massa suspensa, em movimento oscilatório'', leva para realizar o movimento de ida e de volta. Usualmente se representa pela letra T. No Sistema internacional de unidades (SI), o período é medido em Segundos (s).

Assim, o período é o tempo(T) de um ciclo completo de uma oscilação de uma onda.

Freqüência

A freqüência pode ser definida como ''uma grandeza física associada a movimentos de característica ondulatória'' que indica o número de revoluções (ciclos, voltas, oscilações, etc) por unidade de tempo. É possível medir o tempo decorrido para uma oscilação em particular, chamado período (T). Assim, a frequência é o inverso do período, ou

f = 1 / T

Cada padrão de oscilação de um determinado meio corresponde a uma determinada freqüência chamada harmônico.

Imaginemos uma corda de violão, as suas freqüências de vibração variam conforme o comprimento da corda (Por exemplo) e com as suas características (material, tensão, espessura), que determinam a velocidade de propagação das ondas. À freqüência mais baixa de vibração da corda é chamada freqüência fundamental.

Quando temos a deformação da corda, ocorre que a perturbação propaga-se por toda a sua extensão, assim a onda se propagada e reflete nas extremidades fixas. Se ocorrer interferência entre as várias ondas, resultará numa onda estacionária, ou seja, ocorrerá um padrão de oscilação caracterizado por nodos onde não há movimento. Estes resultam da interferência (destrutiva) entre a crista e o vale de duas ondas. Nos anti-nodos, onde o deslocamento é máximo, a interferência ocorrerá entre duas cristas ou dois vales de onda.

Na figura embaixo temos a oscilação de uma corda e seus segundo e terceiro harmônicos.

Ondas estacionárias:

Ondas Estacionárias se formam quando duas ondas idênticas se encontram, se movendo em sentidos opostos, são caracterizadas por pontos fixos de valor zero, chamados ''nodos'', e pontos ''máximos'' também fixos, chamados de ''antinodos''. Aquelas são resultantes da superposição de duas ondas de mesma freqüência, mesma amplitude, mesma direção, porém em sentidos opostos. Mecanicamente se pode obter uma estacionária através de uma corda fixa numa das extremidades e oscila-se a outra extremidade com movimentos verticais periódicos, produzindo-se perturbações regulares que se propagam pela corda. A oscilação, ao atingir a extremidade fixa, se reflete, retornando com sentido de deslocamento contrário ao anterior. Dessa forma, as perturbações se superpõem às outras que estão chegando à parede, originando o fenômeno da onda estacionária, que se caracteriza pela amplitude variável de ponto para ponto, isto é, há pontos da corda que não se movimentam (amplitude nula), chamados nós (ou nodos), e pontos que vibram com amplitude máxima, chamados vales ou antinodos. Entre os nós, os pontos da corda vibram com a mesma freqüência, mas com amplitudes diferentes, assim, estando em repouso, não pode haver passagem de energia , consequentemente, numa corda estacionária o transporte de energia é nulo.

Considerando o comprimento de onda, temos que:

* A distância entre dois nodos consecutivos é :

2 /

* A distância entre dois vales consecutivos é:

2 /

* A distância entre um nodo e um vale consecutivo é:

4 /

Assim temos que:

.

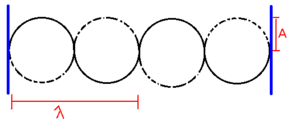
A onda estacionária em uma corda representada pela soma das amplitudes das ondas que formam os antinodos (interferência construtiva)

.

Veja na animação abaixo a representação de uma onda estacionária:

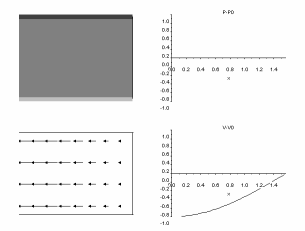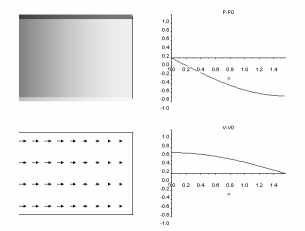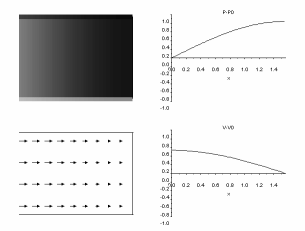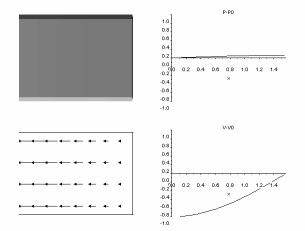
Veja também assuntos relacionados com energia eletromagnética e Física da Atmosfera e interação Terra-Sol:

> A História, Energia, Matéria, Íons, Plasma

> A Atmosfera e a Ionosfera,

> A Troposfera e a Ionosfera >

> Fontes de Ionização 

> Manchas Solares

> Cinturão de Van Allen 

> Ciclos Solares.

> A, K Solar Index

>Ionização na alta atmosfera

> Ionização  

> Recombinação

> Ionogramas >

> Formação de camadas ionizadas