
Modul 1. Bilangan Kompleks itu apa yach...?
Sebelum kita mempelajari bilangan kompleks, ada baiknya terlebih dahulu mempelajari persamaan kuadrat.
2x2 + 3x − 5 = 0
x2 − x − 6 = 0
x2 = 4
Untuk menemukan nilai x didapat melalui rumus ABC atau melakukan faktorisasi.
Ada 3 gambaran dalam mengerjakan persamaan kuadrat:
1. Dengan 2 akar x
Kita bisa menyelesaikan persamaan melalui rumus ABC, yaitu:

Kita mendapatkan 2 akar x, atau melalui grafik persamaan kuadrat y = 2x2 + 3x − 5 memotong sb x di x=-2.5 dan x=1

Berikut ini tambahan contoh dengan 2 akar x:
x2 = 4 mempunyai 2 akar x yaitu, x = -2 and x = 2.
x2 − x − 6 = 0 mempunyai 2 akar x yaitu, x = -2 and x = 3.
2x2 + 13x − 7 = 0 mempunyai 2 akar x yaitu, x = -7 and x = ½.
2. 1 Akar x saja/ akar kembar
Contoh: 4x2 − 12x + 9 = 0
Perhatikan bahwa dengan rumus ABC dimana D = 0, sehingga kita dapatkan 144 − 144 = 0.

Jadi kita mendapatkan 1 akar X saja atau akar kembar, dan kita menyebutnya sebagai akar berulang (repeated root), dimana sebenarnya secara normal adalah 2 akar x.
Kita bisa melihat di grafik y = 4x2 −12x + 9

3. Tidak ada akar yang real
Contoh: x2 −4x + 20 = 0

Contoh tersebut memberikan kita masalah. Melalui persamaan kuadrat kita mendapatkan √(-64), dan seringkali kita diberitahu oleh guru kita bahwa akar negatif tidak bisa diselesaikan. Dapatkah kita menemukan akar negatif tersebut???
Summary:
Persamaan Kuadrat memiliki paling banyak 2 akar yaitu 2 akar real, 1 akar kembar atau akar negatif
Persamaan kubik (pangkat tiga) memiliki paling banyak 3 akar yaitu 3 akar real, 1 akar kembar atau akar negatif.
Contoh:
x3 − 2x2 − 5x + 6 = 0 mempunyai jawaban x = -2, 1 and 3.
x3 = 8, jawabannya = 2, tetapi kita mengharapkan jawabannya ada 2 lagi, dimanakah ...?
Apakah yang dimaksud bilangan Kompleks?
Mau tahu bilangan kompleks itu apa...?
Sabar yach..., kita harus mempelajari apa itu bilangan imajiner. Bilangan imajiner ditemukan sekitar tahun 1800-an, dengan konsep:
√(-1) disimbolkan dengan j
j = bilangan imajiner
Kenapa tidak disimbolkan dengan i ?
Banyak buku yang menggunakan i sebagai simbol bilangan imajiner, karena pengertian i dianggap sebagai kuat arus di fisika maka untuk menghindari kebingungan digunakan j
Contoh:
Anggap (√a)2 = a
, maka
j = √(-1)
j2 = (√-1)2 = -1
j3 = j2(j) = -j
j4 = j3(j) = -j(j) = -(-1) = 1
j5 = j4(j) = 1 × j = j
j6 = j5(j) = j × j = -1 etc
Bagaimana sudah mulai mengerti mengenai bilangan imajiner ???
Coba yang ini...
√(-7) = .........
√(-2)√(-18) = .......
√(-2 × -18) = ......
Bilangan Kompleks
Bilangan kompleks terdiri dari bilangan real dan bilangan imajiner. Oh ternyata gampang yach....?
Contoh:
5 + 6j, 5 = bilangan real dan 6j = bilangan imajiner
-3 + 7j, -3 = bilangan real dan 7 j = bilangan imajiner
Kita bisa menulisnya -3 + 7j atau 7j -3
Kembali ke persamaan kuadrat tadi, apakah kita bisa selesaikan persamaan tersebut ....
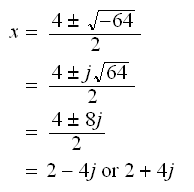
Ada 2 bilangan kompleks ekuivalen x + yj and a + bj, maka
(x = a) dan (y = b).
Contoh:
3 + 2j = a + bj. a = 3 dan b = 2
Coba yach disimbolkan dengan j ....
 =.......
=.......
 =........
=........
j2 − j6=...............
 =............
=............
Format Bilangan kompleks
| |
|
Example |
| Rectangular form: |
x + yj |
5 + 6j |
| Polar form: |
r(cos θ + j sin θ) |
8(cos24° + j sin 24°) |
| Exponential form: |
rejθ |
6e2.5j |
Sampai bertemu di modul berikutnya.
Apabila menginginkan modul lainnya, dapat menghubungi kami.
" if better is possible GOOD is NOT enough "
(Andrie Wongso)
Hubungi:
Ruko Sentra Bisnis Blok C2
Jl. Tanjung Duren Raya No.8
Jakarta Barat
Telp: (021) 5651536, Fax: (021) 5647902