Graphing
More General Tangent, Cotangent, Secant, and Cosecant Functions
Using
the same methods as in the last section, we summarize the results.
 and
and

Graph
of 

Period: 
Domain: All real numbers except  ,
,  an integer
an integer
Range: All real numbers
Symmetric with respect to the origin
Increasing function between consecutive asymptotes
Discontinuous at  ,
,  an integer
an integer
Graph
of 

Period: 
Domain: All real numbers except  ,
,  an integer
an integer
Range: All real numbers
Symmetric with respect to the origin
Decreasing function between consecutive asymptotes
Discontinuous at  ,
,  an integer
an integer
The amplitude is not defined for the tangent or cotangent functions.
The graphs of both functions are unbounded both in the positive and negative directions.
They rise upwards forever and shoot downwards forever.
The constants B and C effect a change in the period and the phase shift of both
functions.
 and
and  both have period
both have period
 ,
,
so
 and
and 
complete
one cycle as

varies
from
 to
to 
In other words,
as
x varies from
 to
to 
 is the phase shift
is the phase shift
 is the period
is the period
of these two functions.
See
Examples 1 – 2, pages 495 – 496, of the textbook.
 and
and 
Graph
of 

Period: 
Domain: All real numbers except
 ,
,  an integer
an integer
Range: All real numbers  such that
such that
 or
or 
Symmetric with respect to the y axis
Discontinuous at Discontinuous at
 ,
,  an integer
an integer
Graph
of 
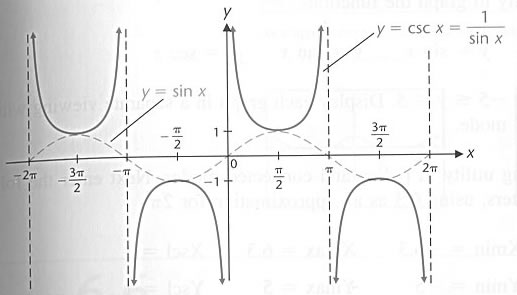
Period: 
Domain: All real numbers except
 ,
,  an integer
an integer
Range: All real numbers  such that
such that
 or
or 
Symmetric with respect to the origin
Discontinuous at Discontinuous at
 ,
,  an integer
an integer
The amplitude is not defined for the secant or the cosecant functions.
The graphs of both functions are unbounded both in the positive and negative directions.
They rise upwards forever and shoot downwards forever.
The constants B and C effect a change in the period and the phase shift of both
functions.
Both functions have period  ,
so (as we did for the sine and the cosine functions) we can
,
so (as we did for the sine and the cosine functions) we can
find the period and the phase shift for each function by solving

and

See
Example 3, pages 498 – 499, of the textbook.
top
next Inverse
Trigonometric Functions



