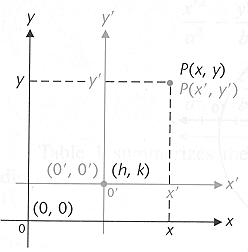Translation
of Axes
Previously, we derived equations for the conic sections
parabola
ellipse
hyperbola
when their axes coincided with the x and y axes of the Cartesian coordinate system
and centered relative to the origin of the Cartesian coordinate axes
Now we will look at the equations of the conic sections when the conic sections
are moved away from the origin of the Cartesian coordinate axes while the axes
of the conic sections remain parallel
to the x and y axes of the Cartesian coordinate system
In other words, we move the conic sections using only parallel translation motions
We will not in any way rotate the conic sections
The equations we will get for these parallel translated conic sections all will
look like
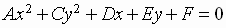
where A and C are not both zero
Translation
of Axes
A translation of coordinate axes occurs when the new coordinate axes
have the same direction as and are parallel to the original coordinate axes
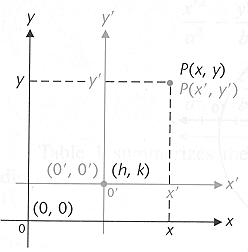
A point P on the plane has two sets of coordinates
(x,y)
in the original coordinate system
(x’,y’)
in the translated coordinate system
Translation
Formulas

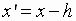
or

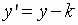
See
Example 1, page 884, of the textbook
Standard
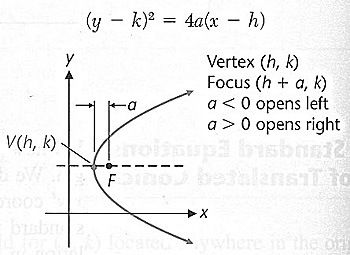
Equations of Translated Conic Sections
Parabolas
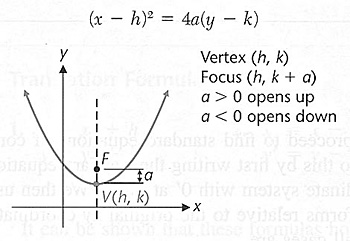
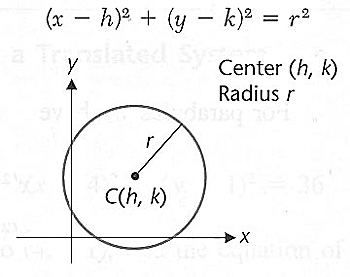
Circle
Ellipses
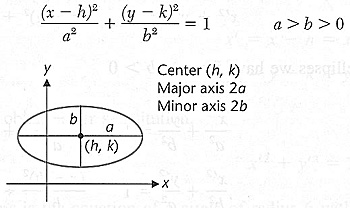
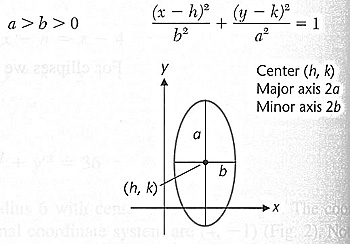
Hyperbolas
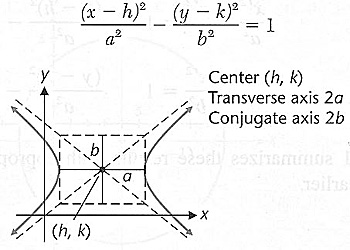
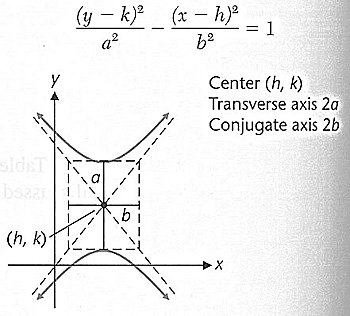
Graphing Translated
Conic Sections
The graph of an equations of the form
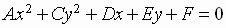
where A and C are not both zero is
a conic section
or
a degenerate conic section
or
there is no graph
If we can transform the equation into one of the standard forms,
then we can quickly identify its graph and sketch it
The method of transforming the equation is the process of completing the squares
See Examples 2 – 3, pages 887 – 889,
of the textbook
Finding Equations
of Conic Sections
Given certain information about a conic section in rectangular coordinates,
we can find its equation
See Example 4, pages 890 – 891, of the textbook
top
next Systems
of Linear equations and Augmented Matrices
begin
Module 5
Systems
of Equations Matrices