Intersection of Cone with Slope of Roof
Links to related geometry and calculators ...
Sloped Frustum of a Pyramid or Cone Calculator
Layover Rafters intersect Main Roof at an Irregular Plan Angle Calculator
Sloped Frustum of Pyramid Calculations for Polygons or Cones by SBE Builders
|
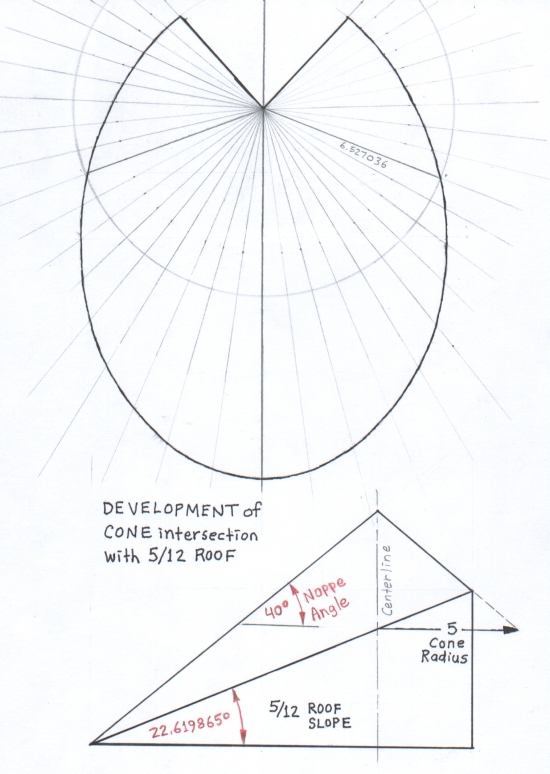
Right Circular Cone Radius = 5
Right Circular Cone Height = 5 × tan 40° = 4.195498 Length of Right Circular Cone Nappe = 5 / cos 40° = 6.527036 Total Angle subtended by ½ Development(s) = 180° × 5 / 6.527036 = 137.888009° 18 datum points of radius 6.527036 define the development of the right circular cone. If the radii are spaced 10° apart, from –90° to +90°, in plan view on the base of the cone, then on the development the ... Angle between Radius Vectors = 137.888009° / 18 = 7.660445° = 10° × 5 / 6.527036 = 7.660445° Datum points on the development of the elliptical frustum were determined using 18 radius vectors following the nappe(s) of the cones(s). (The nappes and radius vectors for both cones are superimposed, refer to the development above). Where x, y and z are points on the ellipse following the surface of the 5/12 roof, the origin being the intersection of the height of the right circular cone and the surface of the roof ... |

|
Ellipse following surface of 5/12 Roof
Major Axis = 14.378797 Minor Axis = 11.520736 Focus = 4.301815 Ellipse Centroid – Circle Center = 3.569996 Ellipse projected to Plan View r = κε / (1 + ε sin θ) Major Axis = 13.272735 Minor Axis = 11.520736 Focus = 3.295381 κ = Focus to Directrix distance = 10.069196 ε = F/b = 0.496564 |
Intersection of 40° Cone with 5/12 Slope of Roof



Changing the Slope of the Roof
Graphs of the Conic Sections in Plan View as produced
with the WZ Function Grapher created by Walter Zorn

Polar Equation of a Conic Section
Focus at the Origin
r = κε / (1 + ε sin θ)
|
Distance from Focus to Directrix
κ = Cone Radius × tan Nappe Angle / tan Roof Slope Angle Eccentricity of the Conic Section ε = tan Roof Slope Angle / tan Nappe Angle The slopes in the numerator terms κε cancel, leaving only the Cone Radius. The equations of the conic sections in Plan View, where the Cone Radius = 5 and the Nappe Angle = 40°, are ... Roof Slope Angle = 0° ... Circle ε = tan 0° / tan 40° = 0 r = 5 / (1 + 0) = Cone Radius = 5 Roof Slope Angle = 22.619865° ... Ellipse ε = tan 22.619865° / tan 40° = .496564 r = 5 / (1 + .496564 sin θ) Roof Slope Angle = Nappe Angle = 40° ... Parabola ε = tan 40° / tan 40° = 1 r = 5 / (1 + sin θ) Roof Slope Angle = 50° ... Hyperbola ε = tan 50° / tan 40° = 1.420277 r = 5 / (1 + 1.420277 sin θ) |
to the Section View of the Cone and Roof Slopes

|
The Cartesian co-ordinates of points on the plan view conic sections are ...
(x = r cos θ , y = r sin θ)
The plan view dimension for y is projected to the plane of the roof using the relation ... y' = r sin θ / cos Roof Slope Angle ... y' being measured on the surface of the roof on a line at a right angle to the x-axis. |
Supplementary Data ...
Cartesian Dimensions for Conic Sections in Plan View
|
ELLIPSE
κε = 5 ε = .496564 κ = 5 / .496564 = 10.069196 = a/ε – aε on y-axis … a = κε / (1 – ε²) = 5 / (1 – .496564²) = 6.636368 on y-axis … Focus = aε = 6.636368 × .496564 = 3.295381 on x-axis … b = Ö(a² – Focus²) = Ö(6.636368² – 3.295381²) = 5.760368 Vertex (from Focus) = a – Focus = 6.636368 – 3.295381 = 3.340987 |

|
PARABOLA
κε = 5 ε = 1 κ = 5 Height = Vertex (from Focus) = 2.5 Width = 2 × 5 = 10 y = – ax² + c c = Height a = – 4 × Height / Width² = – 4 × 2.5 / 10² = – .1 Focus (from Vertex) = Width² / (16 × Height) = 10² / (16 × 2.5) = 2.5 |

|
HYPERBOLA
κε = 5 ε = 1.420277 κ = 5 / 1.420277 = 3.520440 = aε – a/ε on y-axis … a = κε / (ε² – 1) = 5 / (1.420277² – 1) = 4.915518 on y-axis … Focus = aε = 4.915518 × 1.420277 = 6.981397 on x-axis … b = Ö(Focus² – a²) = Ö(6.981397² – 4.915518²) = 4.957579 Vertex (from Focus) = Focus – a = 6.981397 – 4.915518 = 2.065879 |

Projection of Ellipse to surface of 5/12 Roof
and solution of its Focus-Directrix Equation
|
on y'-axis … a' = 6.636368 / cos 22.619865° = 7.189399
Focus (from Centroid) = Ö(a'² – b²) = Ö(7.189399² – 5.760368²) = 4.301815 Ellipse on surface of Roof: Centroid to intersection with Level Plane = Projection of Plan Ellipse Focus to surface of Roof = 3.295381 / cos 22.619865° = 3.569996 Ellipse on surface of Roof: Focus to Level Plane intersect = 3.569996 – 4.301815 = – .731819 ε = Focus / a' = .598355 κ = a' / ε – a'ε = 7.189399 / .598355 – 7.189399 × .598355 = 7.713461 κε = 7.713461 × .598355 = 4.615388 r = 4.615388 / (1 + .598355 sin θ) CHECK … if θ = arctan (– .731819 / 5) = – 8.326903° r = 4.615388 / (1 + .598355 sin (– 8.326903°)) = 5.053276 r cos (– 8.326903°) = 5.00000 = Cone Radius r sin (– 8.326903°) = – .731819 = Focus to Level Plane intersect |