
| Puede fallar |
| experimentos de física y química para hacer con lo que tengas en casa |
Ultima actualización, Martes 06 de Abril de 2004
| En otras páginas | Experimentos de: Mecánica y rozamiento |
| xxxxxxxxxxxxxxxxxxxxxxxxxxxxxxxx Experimentos de:
Videos científicos Jugá al ahorcado |
|
Experimentos
con rozamiento
MATERIALES: mesa, caja de
cartón o bandeja de plástico, cinta adhesiva, hilo de coser,
Vasito descartable, tabla de madera de 20x50 (aproximadamente),
trasportador (sólo si sabés medir ángulos), bolitas o botones
(más o menos del mismo peso)
PROCEDIMIENTO:
|
 |
| Veamos lo que pasa con más detalle. Tanto la base de la caja (roja) como la superficie de la mesa (verde), tienen cierto grado de rugosidad (aunque a simple vista nos parezcan planas). En la figura la rugosidad se representa como los "dientes" de un engranage muy irregular. Estos dientes se encastran mas y mas a medida que agregamos peso en la caja impidiendo que se mueva fácilmente cuando tiramos de ella. La fuerza de arrastre se representa como una flecha negra. Aparece por lo tanto una fuerza de rozamiento que en la figura es la flecha roja que apunta |  |
| a
la izquierda. Mientras la caja no se mueva estas fuerzas
son iguales y el rozamiento se denomina estático. Aumentemos la fuerza de arrastre agregándole un poco de agua al vaso (o algunas bolitas) . Si la caja no se mueve es porque la fuerza de rozamiento estático tambien creció y se igualó a la fuerza de arrastre. Si seguimos agregando agua al vaso llegará un punto en que la caja comenzará a moverse. En ese punto la fuerza de rozamiento habrá alcanzado su valor estático máximo. Su valor es igual al peso del vaso. Ahora la caja se mueve. Eso no quiere decir que el rozamiento desapareció sino que la fuerza de arrastre es mayor que la fuerza de rozamiento. El rozamiento todavia existe pero se denomina dinámico. El valor de la fuerza de rozamiento dinámico (flecha verde en la figura) es menor que el de la fuerza de rozamiento estática máxima. |
|
Podemos encarar nuestro estudio del rozamiento desde otro ángulo. Para ello vamos usar la cajita con las bolitas y una tabla mas o menos lisa que ubicaremos sobre la mesa.
|
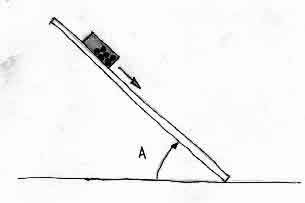 |
Vamos a aprovechar que tenemos bolitas y una tabla hacer un último experimento que tiene que ver con el fenómeno de las avalanchas (objeto de otra sección) pero tambien con el rozamiento.
|
 |
| Si no encontrás ninguna relación entre la experiencia anterior y el desarrollo de una avalancha, mirá el grafico a la derecha. Las bolitas podrian ser los granos de una pila de arena o las piedras en la ladera de una montaña. Identificamos a una en particular pintándola de rojo. Esta claro que en el dibujo A la bolita esta bien "atascada" y no se cae. Igual que en la experiencia con el escarbadiente. Pero si se aumenta el ángulo de inclinación de la ladera, como sucede en la figura B, la bolita roja se libera y cae. | 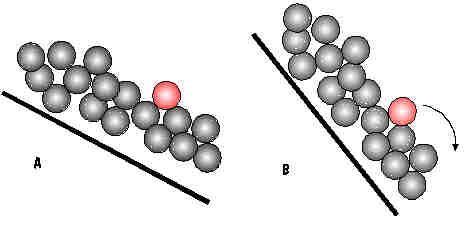 |
| Al caer
adquiere cierta velocidad y por lo tanto cierta energia.
Es posible que esta energia sea suficiente para
"liberar" a otras bolitas de mas abajo cuando
choca con ellas. Y estas liberarán a otras y asi,
iniciándose una avalancha. Claro que para que esto pase
no es suficiente con que una bolita se libere. Ademas
deben ocurrir otras cosas, como por ejemplo que el
ángulo de inclinacion sea de un valor determinado, etc. Una pila de arena es un medio granular como puede ser un montoncito de azucar, cafe molido o fideos municiones. Si querés ver algunas experiencias caseras en medios granulares entrá acá. |
|
MATERIALES: 3 metros de hilo, dos tuercas grandes iguales o dos objetos pequeños y pesadas, dos sillas con respaldo.
PROCEDIMIENTO:
|
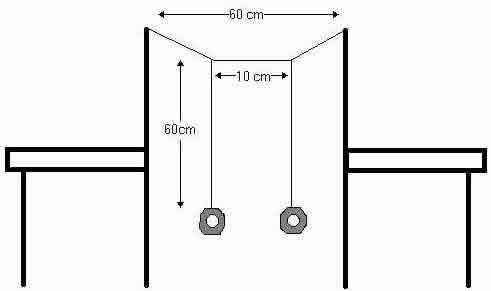 |
Vas a observar un fenómeno muy curioso e interesante.
El primer péndulo oscilara durante unos instantes movido por la energía que le imprimiste al sacarlo de su posición de equilibrio. Al cabo de un tiempo comenzará a frenarse gradualmente. Vas a notar que conforme esto pasa, el segundo péndulo comienza a oscilar y la amplitud de sus oscilaciones aumenta. Sucederá que el primer péndulo se frene por completo mientras que el segundo oscile con la máxima amplitud como si le hubiera "absorbido" por completo la energía del primer péndulo.
Para fanáticos: hacé click acá para más detalles sobre el problema de los péndulos acoplados: ecuaciones, soluciones, graficos, etc.
| Y más! El Ing. Daniel Abraham (docente de la Fac. de Ingenieria UBA, nos ilustra sobre el problema de dos resortes acoplados en el que también se presenta el fenómeno de intercambio de energia. Se puede bajar un macro en Excel que permite seleccionar los parámetros del problema y obtener las soluciones correspondientes. Hacé click acá. |