
Revision Date: July 9 2002
This unit consists of chapters 3, 4 & 5 in your text book
Chapters 1 & 2 are a review of the Grade 10 Motion Strand
This chapter is essentially a review of last year's motion strand and should be treated as such. The key to this unit will be doing the assigned homework!
In case you forgot anything here's a set of Internet notes to brng you up to up to stream Review is Here
Scalar quantities have only a size or magnitude associated with them.
Vector quantities besides having a magnitude have a direction associated with them.
Distance is a scalar quantity. It only has size. The length of your desk would be a distance. The width of a hockey arena is a distance. Direction not required.
Vector quantities are represented graphically by a line which has the required magnitude and line is pointed in the given direction based on standard compass points of N, E, S, & W in this clockwise order.
The line drawn has a starting point (tail) and an end point (tip) which has an arrow head attached to it. The line has a length (magnitude) and an angular displacement (direction)
Displacements are generally drawn in a scale diagram to represent the actual distance.
The quoted angle that I will use will always be described from either the North or South axis pointing towards either the East or West axis, with the displacing angle in between.



Velocity comes in several different modes or types. There is constant or uniform velocity, average velocity, instantaneous velocity and finally non-uniform or changing velocity. Guess what? you have to be able to tell them all apart! You should already know what these are, but if you don't, either listen in class or see pages 13, 15, 21, & 22. see page 49 for SS students
A special type of problem which I will call the navigation problem relatates velocity to displacemant vectors and are added as such. Several problems done in class.
Velocity is a vector, speed is a scalar. Being a vector velocity besides having a magnitude will have a direction associated with it.
Slope of lines convey different things. Slopes can only be found for straight lines. Slopes are either positive, zero or negative. Make sure you know what each means!
A tangent is a straight line that touches a curve at only one point. The slope of this line is called the instantaneous velocity at that point.
Acceleration is defined as the rate of change of velocity over a defined time interval. Acceleration is a vector and points in the same direction as the motion. Acceleration can be constant (non-zero), which means that the velocity will be changing. The acceleration itself may be changing, which yields a much more complex motion study.
Accleration is usually plotted against time resulting in either a straight line or a curved line, ususally in the shape of a parabola.
Average and instantaneous accleration are dealt with the same way as average and instantaneous velocity.
Here's the set of motion equations that must be known

You must be able to use these equations in any and all circumstances.
You should recognize that equations 6 & 7 are quadratic equations in nature.
There are four fundamental forces of nature: gravity, strong nuclear, weak nuclear and electromagnetic. In this chapter we are concerned with what these forces can do to to an object.
A force is defined as a push or a pull. When a force acts on an object it may cause the object to move or change its motion. A force is a vector quantity having magnitude and a direction
in which it either pushes or pulls. When a body is put in motion because of a force the velocity of this body is in the same direction as the force.
The units for force is the newton which is a short form for a kilgram-meter per second squared. 1N = 1 kg-m/s2.
Forces can be measured with a spring scale, which is usually calibrated to the force of gravity acting on masses of known weights. Their is a relationship between the mass of an object
and the force of gravity acting on it. (Dealt with later.)

Vector addition techneques are used for any vector. Vectors have magnitude and directions and when adding both must be taken into account.
A vector diagram as seen in Fig 1. shows the addition of V1 to V2. The end of V1 or arrowhead becomes the starting point of
V2. Connect the starting point of V1 to the end point of V2 and measure the magnitude of this resultant vector called V3.
Measure the angle from the north axis and report the angle as [N E].
from the north axis and report the angle as [N E].
The addition may be carried out using trig. V3 may be dermined by using Pythagorean theorem and calculating the size of V3. To find the necessary
angle use (tan )-1 = V2/ V1 and solve for the angle. Don't forget to report the answer in the correct fashion.
)-1 = V2/ V1 and solve for the angle. Don't forget to report the answer in the correct fashion.
Resolution of vectors is the undoing of two added vectors. Fig 2. has vector V being projected onto the horizontal and vertical axis (in yellow). The dotted lines are the projections of V
onto each axis. Vh is the horizontal vector component and Vv is the vertical component. To find Vh and Vv get out
your ruler and measure the magnitude of the lines. Vh as shown in Fig 2. has an [E] direction and Vv has a [N] component.
If you where to add Vh to Vv the answer would be V.
Trigonmetry can also be used to find both Vh and Vv. Angle  is a given value in the problem therefore Vv = cos
is a given value in the problem therefore Vv = cos V and
Vh = sin
V and
Vh = sin V.
V.
Projectile motion using vector resolution will be discussed in class. Any object that follows a parabollic trajectory has a horizontal velocity and a vertical velocity that are added together and the resultant velocity is the one observed. To work the system you must resolve this velocity vector into its two components. This is because different forces are acting on the object in each direction.
Question done on the board to cover different situations.
Relative motion occurs when an object has two forces acting on it in different directions. This results in the velocity of the object being effect by both forces and vectory addition must be used to arrive at the answer.
Forces can be represented by line segments which have magnitudes and directions. A free body diagram will encompass all forces acting on a body ususally from a central point of the
body (in actual fact the so called center of gravity of the body is where all forces appear to be acting on or from).
There are two general types of net forces which act on a body: balanced forces and unbalanced forces. A free body diagram properly labeled will
dictate which of the two types of net forces is acting on the body (book say this a tiny bit different).
The adding of collinear and non-collinear forces will be dealt with in class.
Newton's Law of Universal Gravitation is covered in the text book page 68.
Changes with gravitional field intensity will be mentioned in class.
In the study of vectors we saw that two vectors perpendicular to each other may be added either using a scaled geometric diagram or applying trig relations based on a right angled triangle.
The problem can be reveresed by giving you the resultant vector (the hypothenuse) and you determine the two sides of the triangle either by a drawing or using trig. This principle of vector resolution yields the horizontal and vertical component of a vector, which can be used to solve motion problems in which the force is acting in only one direction yet the motion is in two. Such a problem is the "hang time" in which an object is thrown into the air as some angle and you determine how ling it will remain in flight and how far it travels.
Friction is a force that opposses the motion of an object when an object slides across another surface or travels in any fluid. Terms that you should be familiar with are: sliding friction, rolling friction, limiting static friction, kinetic friction, normal force . These terms are found in the text book pages 92, 93, & 94.
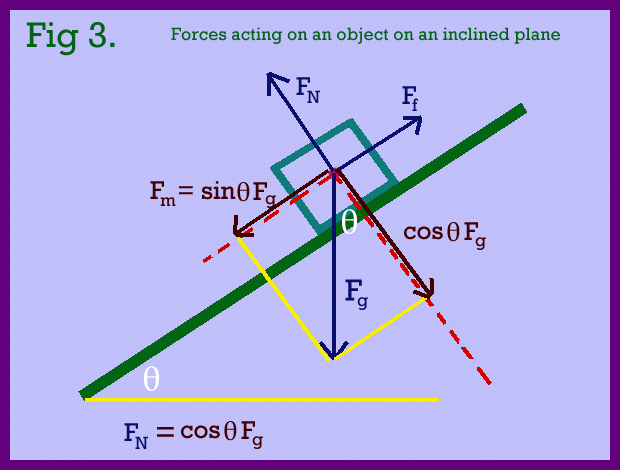
Forces acting on an object on an inclined plane are shown in Fig 3. Identification of forces as follows:
 Fg
Fg
 Fg
Fg
 : is the angle of the inclined plane
: is the angle of the inclined plane
Friction occurs when a body slides across a surface and is a reactionary force, that is, it opposes the applied force and acts in the opposite direction of the motion. Three situations do arise and are list below:
 Fg and Fm has a value of
sin
Fg and Fm has a value of
sin Fg.
Fg.  the greater the value of Fn and the less value of Fm. The greater the angle the greater Fm
and the greater the probability that the object will slide down the ramp.
the greater the value of Fn and the less value of Fm. The greater the angle the greater Fm
and the greater the probability that the object will slide down the ramp.
The coefficient of friction whether kinetic or static is the ratio of the frictional force Ff to the normal force Fn.
A graph of force of friction versus normal force will yield a straight line with a slope equivalent to coefficient of friction. (See page 94 for such a graph).
Kinetic friction is equivalent to (but in the opposite direction) the force needed to keep body moving at a constant speed.
Static friction is the force needed to start an object moving and is greater than the kinetic force.
Coefficients of friction are a function of the two surfaces that are in contact with each other. A table of such values is found on page 96.
Usually the math problems are straight forward and use the coefficient of friction equation found on page 95 of the text. The interesting problem occurs when used with the inclined plane where Fn has to be evaluated using either a geometric diagram or a trig expression and the mass of the body sitting on the inclined plane.
Inertia is defined as that property of matter that resists changes to its state of motion or when it is at rest. Inertia is a resistance to a change in motion, whereas friction is a resistance to that motion. Remember a body at rest will stay at rest, a body in motion will stay in motion, unless acted upon by some external force. This is not extremely obvious on Earth because all motion is subject to some from of friction which is an external force an will act in opposition to any appllied force or motion. The above statment is essentially Newton's First Law of Motion. See page 104 for the text book definition.
When a force acts on an object, this object will accelerate in the direction of the applied force. As long as the force is applied the object will accelerate. A bullet fired from a rifle will
accelerate down the barrel of the rifle. Once it leaves the barrel, the applied force of the chemical explosion is not longer present and the bullet will now gradually slow down due to air resistance. Actually the bullet will either strike some object or fall to the ground long before air resistance will stop its motion. Gravity will act on the bullets vertical motion but will not effect its horizontal motion.
The mass of an object is also part of the equation. Throw a baseball then try to throw a bowling ball. Which can you throw farther? The applied force which cames from you arm muscles is
the same in both cases. The baseball will achieve a greater acceleration and travel further. The only difference if the mass of each ball.
Newton's Second Law is stated on page 108 of the text, and so is the equation theat relates the three variables; mass, acceleration, and force. F = ma. Remember that F is actually the net force acting on the object.
The Law itself is simple and straight forward to use. Additions to a problem include
Forces always occur in pairs. The action force and the reaction force. Whenever one object exerts a force on another or second object, the second object exerts a force on the first object will an equal magnitude but in the opposite direction. So who wins this apparent pushing contest? Lets look at a couple of examples.
Section 3.5 of the text deals with numerical motion problems and Newton's Laws. Examples will be dealt with in class