‘IT IS HARD.’ WHY IS TRIGONOMETRY IMPORTANT?
 
It really isn't hard. If it seems hard that's because you were taught in a manner that doesn't work for you. Different 
people learn different ways, but teachers sometimes only teach one way (whatever way they are best at), whereas the 
way you are taught needs to be the way you learn. One of the main things that need to be taught when you learn 
something is what it's good for and what you need it for. If that wasn't part of what you learned, then that is probably 
why you don't understand it.

 

 

The reason why trigonometry is so important lies all around us everyday, although most of us are blissfully unaware

of what trigonometry does for us in our lives.  It would not be possible to build a car without trigonometry. The

homes we live in are built using trigonometry. Just about every piece of technology we take for granted is researched, developed, and manufactured based on some trigonometric knowledge somewhere along the line.

 

 

Navigation and surveying are also heavily dependent on trigonometry. Without it, we would never have been able to

send men to the moon since we need trigonometry to compute launch trajectories, orbital trajectories, and re-entry

trajectories. Thanks to our knowledge of trigonometry, we can build concert halls filled with the incredibly rich and

complex sounds of a symphony orchestra. Much of our knowledge about waves (sound, light, water, etc…) comes

from trigonometry.

 

 
So, is trigonometry important? Definitely a resounding YES! Learn it, know it, and use it to enhance your life. 
Theoretically, you could go through life completely ignorant of what trigonometry is capable of doing for you. You 
could have no knowledge of trigonometry, or any mathematics. Many people do. The drawback to such a life is that 
one is then not able to understand the wonders that nature has to offer.  
 
 
Trigonometry is necessary any time there is an angle involved (the angle of the sun, the angle of the cue ball in a 
game of pool...) or any time you have to compare two non-parallel lines (the height of a building and the height of its 
shadow, the distance a train is from the crossing and the distance a car is from the crossing). These kinds of 
problems cannot easily be solved without trigonometry.
 
 
But what is trigonometry? There are only three important definitions in trigonometry. Everything else is based on those three. If you can understand these three definitions, you should have no trouble understanding any other part of 
trigonometry.
 
 
First, consider a triangle with a right (90-degree) angle: Label the side that doesn't touch the right angle as the 
hypotenuse. Now one of the remaining sides is touching your angle. That is the adjacent side. And the other one? The 
other one is the side opposite to your angle. Now your triangle looks like this:             
 
The three most important trigonometric functions are: sine, cosine and tangent. Now here are the three most important formulas:
 

                                                                        

Name

Equation

 Sine of a

Cosine of a

Tangent of a


Connections

 

Arts

While studying trigonometric functions, students can learn how mathematics is related to tuning stringed instruments such as guitars.

 

Science

While studying trigonometric functions, students can discover the periodic relationships that occur in pendulum and spring motion, heart rates, and radio frequencies.

 

Technology

While studying trigonometric functions students can perform experiments using computer assisted data gathering devices and graphing calculators to determine appropriate algebraic representations for the data.

 

For instance, a typical problem might be: you want to measure the height of a building without climbing it. So, you stand thirty feet away from the building, and you measure an angle of elevation of 60o to the building top. How tall is the building? To start any such problem, draw a picture. Make sure you label all the relevant angles and sides. 

 
Now, look at which sides are important. In this case, the side you know is adjacent to the known 60o angle; 
and the side you want to know is opposite the angle. This tells you which trig function you want: the tangent, 
since it relates the opposite and adjacent sides and ignores the hypotenuse. From here on, it's easy. 
Use a calculator or trig table to tell you that tan 60o = 1.73. Then write tan µ = opp/adj and you can write the 
equation 1.73 = ht/30'. Solving, ht = 51.9 ft. without leaving the ground, you have measured the height of a 
building very exactly: simply by knowing that the ratio tan µ = opp/adj is the same for a gigantic 
building-person-cement triangle. 
 
 
Another example, use trigonometry to figure out the distance across rivers.

We first set up a survey post directly across the river from some landmark (like a tree). Then we head downstream a distance that we can measure; in this case, 400 meters. That's the red horizontal line in the drawing. Now we take a sighting on the tree from downstream. That's the black line in the drawing. The surveying instruments will tell us what our sighting angle is. In this case, it's 31 degrees. The tangent of 31 degrees is equal to the length of the blue line divided by the length of the red line (400 meters). So, if we multiply the tangent of 31 degrees by 400 meters, we'll get the distance across the river. The tangent of 31 degrees is about 0.60. That means that the distance across the river is 0.6 times 400 meters, or 240 meters.

Real world alert! Wouldn't it have been simpler to just tie a rope to the tree, climb into a boat, go across the river, and measure how much rope you trailed out? In this case, it actually might be a good idea to physically cross the river to check the answer from our math. This gives us confidence that trigonometry really works. After all, sometimes the real world gives us a river that is too difficult to cross or a cliff too dangerous to climb. In these cases the physical approach isn't possible. We need trigonometry--a mathematical technique we can trust for the answers we need.

 

Right Triangle: 70o                                                                              window

                                                                                 
                                                      
                                                                             10
                                       
                                      
                                     ladder (l)                             
 
                                                        
 
Imagine this is a ladder is leaning against a wall at an angle of 70 degrees with the ground. It just touches the bottom 
of a window 10 feet off the ground. How long is the ladder (l)? If we wanted to find "l" (the length) we would 
need an equation that involved an angle and the side opposite from it (10) and the hypotenuse side (l).
 
Well, isn't that just the equation for the sine of an angle?
 
sin (µ) = opposite / adjacent => sin (70o) = 10 / l
 
Now, using a little algebra (and using * to mean multiplication): 
          
                                          sin (a) = opposite / hypotenuse
                                       sin (70o) = 10 / l
                                   l * sin (70o) = l * 10 / l
                                   l * sin (70o) = 10
                   l* sin (70o) / sin (70o) = 10 / sin (70o)
                                                    l = 10 / sin (70o)
                                                    l = 10 / 0.9397
                                                    l = 10.64 feet

 

The basic problem of trigonometry runs somewhat like this:

an old surveyor’s 
telescope (theodolite)
 
                             
 
 
 
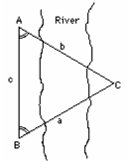
You stand next to a wide river and need to know the distance across it--say to a tree on the other shore, 
marked on the drawing here by the letter C (for simplicity, let's ignore the 3rd dimension). How can this be 
done without actually crossing the river? The usual prescription is as follows. Stick two poles in the ground 
at points A and B, and with a tape measure or surveyor's chain measure the distance c between them 
("the baseline").Then remove the pole at A and replace it with a surveyor's telescope like the one shown 
here ("theodolite"), having a plate divided into 360 degrees, marking the direction ("azimuth") in which the 
telescope is pointing. Sighting the telescope, first at the tree and then at pole B, you measure the angle A of 
the triangle ABC, equal to the difference between the numbers you have read from the azimuth plate. Replace 
the pole, take your scope to point B and measure the angle B in the same way. The length c of the baseline and 
the two angles A and B, contain all there is to know about the triangle ABC--enough, for instance, 
to construct a triangle of the same size and shape on some convenient open field.
 
NON-RIGHT TRIANGLE
But what about a triangle that doesn't have a 90-degree angle? 
What can we do about that? 
This is the generalization of the Pythagorean Theorem to non-right triangles. 
Well, it turns out that any shape can be completely made of right triangles. 
 
 
Consider this triangle:
 
That triangle doesn't have any right angles at all. But it's the same as these two right triangles:
                                                   
So we could do all the algebra and figure it all out, or we could take the shortcut and use the equations 
that other people figure out. 
The most famous one is the cosine law. 
To use the cosine law we need to label our triangle. 
But we can't use hypotenuse so we can't label it the same way. 
So we will use letters instead: 

 

Notice that corresponding letters of the alphabet are the opposite sides to their angles.

That is very important. So side c  is opposite angle C.

The cosine law looks like this:   =>    c˛ = a˛+b˛-2abcos(C)

                                                     =>    b˛ = a˛+c˛-2accos (B)

                                                 =>    a˛ = b˛+c˛-2bccos (A)

Here is a triangle with no 90-degree angles, but we do have enough information to use the cosine law. 
Let's label our triangle so that c is the side that doesn't have a value:
                                                                                                                                
    
 
 
     c2 = a2 + b2 - 2ab cos(C)                                                                                                                                
    c2 = 102 + 82- 2*10*8*cos (20o)                                                                 
    c2 = 100 + 64 - 160*cos (20o)                                    
    c2 = 164 - 160*cos (20o)                                                                                      
    c2 = 164 - 160*0.9397                                                                                               
    c2 = 13.6492                                                                        
sqrt ( c2 ) = sqrt( 13.6492 )      sqrt = square root
    c = 3.6945
 
 
Most of the rest of the stuff is just algebra. Some of the algebra gets messy, but the trigonometry really never gets 
more complicated than this.
 

 

One last note on trigonometry: Although many people think trigonometry is completely divorced from algebra, it really isn't. Trigonometry is an extension of algebraic ideas—functions in particular—to trigonometric concepts. We can often treat trigonometric concepts in algebraic terms. Solving a trigonometric equation is very similar to solving an algebraic equation. Do not be confused by the changes in terminology. And that’s all there really is to trigonometry.

 
 

Home / Trig.1 / Trig.2 / Trig.3 / Trig.4