Function Fundamentals

A function is a rule which maps each x to a unique y.
The domain is the set of all allowable x-values or inputs.
Restrictions on the domain originate from two sources
(i) division by zero
(ii) even roots of negative numbers.
The range is the set of allowable y-values or outputs.
Vertical line test: A vertical line intersects the graph of a function at most once.

Example:     Determine the domain of f(x)=sqrt(5-x) 
To ensure that we take the square root of a negative
number we require that 5 - x ³ 0  OR  x £ 5.
Example:     Determine the domain of f(x) = 1/(x2 + x - 2). 
To avoid division by zero we factor the denominator
f(x) = 1/((x + 2)(x - 1)) and require that x ¹ -2, 1.
Example:     Given the function f(x) = 2 x2 + x - 3 compute f(0) and f(2). 
This is an exercise in using function notation.
Simply substitute in 0 for x and substitute in 2 for x.
f(0) = 2 02 + 0 - 3 = -3
f(2) = 2 22 + 2 - 3 =  7
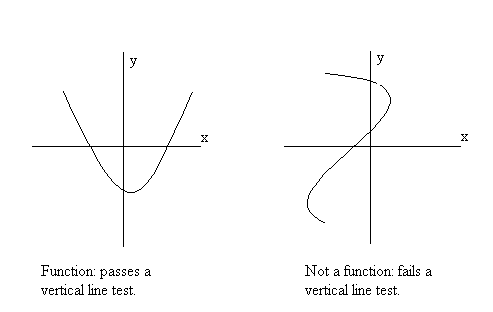
Example:     Determine if the following graphs represent functions. vertical line test

Exercises 




(1) The domain of a function is 

     
The set of allowable inputs into a function.

 
     
The set of outputs from a function.



 


 (2) Determine the domain of  f(x) = sqrt(x-3). 

     
x ³ 0 

     
x > 3 

     
x ³ 3 

     
x £ 3






 (3) Determine the domain of  f(x) = 1/(x2 - 5x + 6) 

     
x is any real number except 0,-2 

     
x is any real number except 0,5 

     
x is any real number except -2,-3 

     
x is any real number except 2,3 





(4) Given the function f(x) = sqrt(x-3)/(x2 - 1) determine f(7). 

     
0 

     
1/12 

     
1/24

 
     
4/49






  

    
    
	(5) Determine if the graph below represents a function  


     
      The graph represents a function. 

     
    The function does not represent a function.		
  

  

    Function or not
    
  








|  Table of Contents  |
|  Previous  |
|  Next  |